マインドマップでノートを変える！ マインドマップって何？その３つの利用方法 マインドマップ１

今日の紹介はマインドマップです。

似たものとしては、イメージツリー、フィッシュボーンなどがあると思いますが、一番自由度が高く、一般的だと思われるので、「マインドマップ」という言葉を使います。

 マインドマップでマインドマップ的思考を身につける

実際にマインドマップを使う練習をしていくことで、「マインドマップ的な思考方法」が身につきます。

この「マインドマップ的な思考方法」というのは、要は整理をしていくということです。

まず、第一レベルの見出し、箱ができる。

その箱の中に入れる、第二レベルの見出し、箱ができる。

そして、また、その中に…ということを繰り返して、山ほどある頭に入れるべきことをすっきりと整理していくことができるようになるわけです。

話してみるとわかりますが、成績の良い生徒というのは、必ず、物事を何らかの方法で「整理」して頭の中に入れています。

それは、歴史のような暗記物だけでなく、国語の要約のようなものでもそうです。

成績の良い生徒は、頭の中に箱や見出しのレベルができていて、逆に、覚えるべきものがすべての点のようになってしまっているとなかなか覚えきれなくなるわけです。

どうやって、こういう思考方法を身につけるか？

その具体的な実践として、「マインドマップを書く」「マインドマップに書き直す」ということをするとよいと思うのです。

というわけで、参考になるのは、トニー・ブザン氏のものでしょう。

 実践を一緒にできるといいのですが、早いのは買うことです。

新版 ザ・マインドマップ(R)

 こちらの方が小学生や中学生にはわかりやすいと思います。

マインドマップ（Ｒ）ｆｏｒ　ｋｉｄｓ勉強が楽しくなるノート術

 すごくおすすめです。実際の絵が多くてわかりやすいです。

マインドマップの実際とポイント

 例を出しますと、こんな感じ。

教科書の単元の見出しだけです。

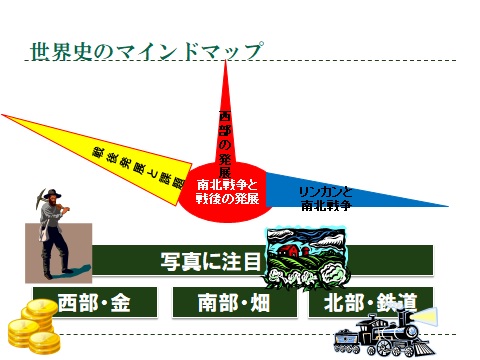
これが世界史の教科書のマインドマップです。最初のマインドマップが、教科書の見出しをまとめ、そのひとつの見出しが次のマインドマップになっています。

今度は見出しを真ん中にもってきて文章がマインドマップになりました。

ポイントは

1. きちんと枝で書くこと
2. 色をつかうこと、そして色の順番を自分なりに決めておくこと
3. 色の数＝枝の数は７を限度に
4. へたくそでいいから、絵を描くこと

というあたりです。

ひとつずつ説明しましょう。

 きちんと枝で書く

 傍線と○で書くこともできますが、こうすると、幹の感覚がなくなります。

太い幹＝第一レベルの見出し、次の幹＝第二レベルの見出し…

ということが大事なんです。だから、ぜひとも三角形のイメージの幹を書いていくようにしてください。

 色を使うこと、そして色の順番を自分なりに決めておくこと

 色を使うことによって、より記憶に残るようになります。そして、使う色の順番を決めておきます。

赤、青、黄、緑、紫、オレンジ、茶色

という風に色の順番を決めておけば、あとで思い出す時に、「○色まで使った」という思い出し方ができます。そうすると、今思い出している見出しレベルがいくつあったかがわかります。

 色の数＝枝の数は７を限度に

 この数は７つが限度です。それは平均的に人間の記憶は７つが限度だからです。

manebi.hatenadiary.jp

７つを越える場合は、見出し＝箱＝分類をして、７つの中におさめるようにすることが大事です。ですから、７つの色の順番を決めればいいわけですね。

へたくそでいいから、絵を描くこと

 このときに、絵を描いておくと、記憶に残りやすくなります。うまい必要はありません。棒と○で人を描く程度でかまいません。自分が何を書いたかわかればいいし、絵が下手だったら、字を足してわかるようにすればいいのです。ほんの一瞬の手間で、記憶を呼び起こすきっかけになります。

 こんなところです。

 マインドマップの活用方法

それでは、マインドマップはどのように使うのでしょうか？

今回は概略だけ説明しますが、大きくわけると次の３つだと思います。

その１　整理・分類して、「覚える」「再現する」

 歴史や地理などの暗記もの、現代文の要約などは、このパターンです。見出しのレベルを意識して、少しずつ細かい枝をつくって整理します。

それを見て覚えて、頭の中で再現して思い出していきます。

 その２　「発想をひろげる」

これは、何かアイディアを出していくための方法です。真ん中のキーワードから、連想する言葉を書き出し、そこから発展させていきます。

応用としては、算数・数学の情報が少ないタイプの問題を変型させて、使えるような形にしていくこともこのマインドマップの応用でできます。数学が普通かややできる子が本当に得意になるためにはこのステップがかけている場合が多いです。

 その３　「逆算をする」

 その２の逆で、ゴール＝目的を中心に書き、そこから逆算して、最初の一手に戻していくやり方です。そもそもは学習計画を立てることなどがこれに当たりますが、応用としては、算数・数学・理科などの途中のステップを立てるためにはこういう練習が必要です。

１・２・３・４と手順を追う問題ならできるのに、いきなり４を求めなさい、となると急にできなくなる生徒はこうした練習が必要です。算数や数学が苦手な子ども向け、という感じです。

とりあえずは以上です。

次回以降はそれぞれのマインドマップの使い方、練習の仕方について、考えてみたいと思います。